Denoising Diffusion Probabilistic Models

(1) Diffusion 류의 모델학습을 새롭게 개발하고 싶다 → 수식 전개 모두 알아야함 (2) Diffusion 관련 연구를 하고, 논문을 읽고 싶다. → 수식의 의미와 흐름 정도 (3) 사용만 하고 싶다 → 수식 몰라도 되고 수식:구현의 매칭만 알면 됨.

1. Introduction

• 최근 심층 생성 모델(Generative Models)이 이미지, 오디오 등 다양한 데이터 형식에서 높은 품질의 샘플을 생성하는 데 성공.
• 대표적인 모델로는 GANs, Autoregressive Models, Flows, VAEs가 있으며, Energy-based Models과 Score Matching 방법도 GAN과 유사한 품질의 이미지를 생성
• Diffusion Probabilistic Models는 비평형 열역학에서 영감을 받아, 점진적으로 노이즈를 추가하는 과정과 이를 역으로 복원하는 과정을 학습하는 모델.
• 작은 가우시안 노이즈를 추가하는 방식이기 때문에, 이를 역추적하는 과정 역시 가우시안 분포로 설정할 수 있으며, 간단한 신경망을 사용해 모델을 학습할 수 있다는 것을 보여줌
• Diffusion 모델은 고품질 샘플을 생성하지만, 다른 확률 기반 모델과 비교했을 때 로그 가능도(log likelihood) 에서는 경쟁력이 떨어짐.
• 즉, 고화질이지만 데이터의 분포를 반영하지는 않는다는 뜻으로, diffusion은 고품질이지만 실제로 존재할 확률이 적은 이미지를 만들어 낸다는 것.
• 그러나 다른 energy based model들 보다는 생성 퀄리티 및 로그 가능도가 더 높음
• 이는 대부분의 정보가 인간이 인식하지 못하는 미세한 이미지 디테일을 설명하는 데 소비되기 때문이라고 함.
• 이러한 특성을 손실 압축 (lossy compression) 관점에서 분석하고, Diffusion 모델의 샘플링 과정이 점진적 디코딩 (progressive decoding) 으로 이해될 수 있음을 설명함 (인데 이해할 수 있을까)

2. Background

Diffusion Intuition

• 왜 diffusion일까? 분자의 확산?
• 물리적으로 분자가 확산될 때, 분자가 모양을 갖추어 갈 때 분자의 움직임은 미시적으로 gaussian 분포를 따른다.
• 그 움직임을 앞으로 해도 뒤로 해도 Gaussian분포를 따른다.
• 그렇다면 원래 상태를 다시 돌릴 수도 있을까?
• 이걸 한번에 예측하기는 어려우니, 단계 단계별로 점진적으로 예측하다보면 결국 원래 상태를 추정할 수 있지 않을까?

Reparametric trick

• Variational Autoencoder (VAE) 같은 모델에서 확률적 샘플링 과정이 포함될 때, 이걸 직접 미분하려 하면 문제가 생김.

• 왜냐면 샘플링 과정이 비결정적(nondeterministic)이라서, 역전파(Backpropagation)가 불가능함.

• Reparameterization Trick을 사용하면, 확률적 연산을 미분 가능한 연산으로 변환 가능.

• 원래 샘플링 방식:

  $z$ $\sim \mathcal{N}(\mu ,{\sigma }^2)$

  → 여기서 직접 $z$를 샘플링하면 미분할 수 없음.

• 대신 Reparameterization Trick을 사용해서,

  $z=\mu +\sigma \cdot ϵ,\text{where }ϵ\sim \mathcal{N}(0,1)$

  → 이렇게 하면 $\mu$와 $\sigma$에 대해 미분 가능해짐.

기호 정의

• $x_0$: 원본 데이터 (예: 깨끗한 고양이 사진)
• $x_{1:T}$: 노이즈가 점진적으로 추가된 잠재 변수들
• $p_{\theta }(x_{t-1}\mid x_t)$: 역방향 과정(Reverse process)에서 $x_t$로부터 $x_{t-1}$을 생성하는 확률
• $q(x_t\mid x_{t-1})$: 순방향 과정(Forward process)에서 $x_{t-1}$로부터 $x_t$로 노이즈를 추가하는 확률
• ${\mu }_{\theta }(x_t,t)$: 역방향 과정에서 평균을 예측하는 신경망
• ${\Sigma }_{\theta }(x_t,t)$: 역방향 과정에서 분산을 예측하는 신경망
• ${\beta }_t$: 시간 단계 $t$에서의 노이즈 수준 (Variance schedule)
• ${\alpha }_t=1-{\beta }_t$: 노이즈의 신호 비율
• ${\bar{\alpha }}_t={\prod }_{s=1}^t{\alpha }_s$: 누적 신호 비율

---

수식 (2): Forward Process, diffusion process

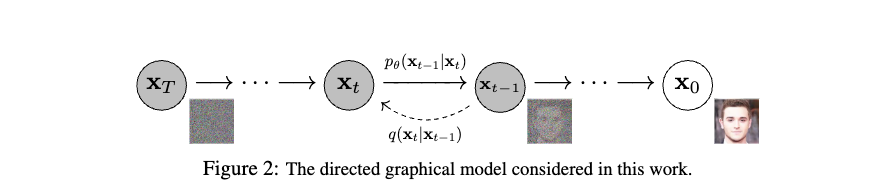
• Figure 2을 역방향으로 수행했을 때, Forward process로써 Noise를 주입함

• (여기서 한가지) 원본에서 지속적으로 Gaussian noise를 더해주다보면 결국 gaussian 분포의 노이즈가 된다는 기존 연구 존재 (ref)

• Markov chain의 성질 현재 상태는 $x_t$는 $x_{t-1}$에 영향만을 받는다라는 가정 하에 원본 데이터 $x_0$가 주어졌을 때, $x_T$가 나올 확률은 아래와 같이 주어질 수 있음.

• 이 과정은 수식적이며 기계적으로 진행될 수 있는 학습의 영역이 아님. $q(x_{1:T}\mid x_0)={\prod }_{t=1}^{T}q(x_t\mid x_{t-1})=q(x_1\mid x_0)\cdot q(x_2\mid x_1)\cdots q(x_{T-1}\mid x_{T-2})\cdot q(x_T\mid x_{T-1})$

• 이때 주입하는 noise는 아래와 같은 분포로 따르게 주도록 되어 있음. ${\beta }_t$는 주어지는 상수값으로 $t$에 따라서 스케쥴링할 수 있음.

• 분산에 붙은 ${\beta }_t$는 noise 절차가 진행되어도 최종 결과는 항상 분산이 1이 되도록 하기 위한 trick이라고 함.

$q(x_t\mid x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$ $x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}ϵ,ϵN(0,1)$

• $x_0$: 원본 데이터 (예: 깨끗한 고양이 사진)
• $x_{1:T}$: 노이즈가 점진적으로 추가된 잠재 변수들
• $q(x_t\mid x_{t-1})$: 순방향 과정(Forward process)에서 $x_{t-1}$로부터 $x_t$로 노이즈를 추가하는 확률
• ${\beta }_t$: 시간 단계 $t$에서의 노이즈 수준 (Variance schedule)

def q_sample(self, x_start, t, noise=None):
 
	noise = default(noise, lambda: torch.randn_like(x_start))
	
	x_t =  (
	
	extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start
	
	+ extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise
	
	)
	return x_t
 

수식 (1): Reverse Process

• Gaussian noise $x_T$로부터 노이즈를 제거해가며 원본 $x_0$ 까지 생성될 확률을 구할 수는 없을까?
• 다르게 표현하면, 이 forward를 해서 이 노이즈 상태가 되었다면, 이 노이즈가 나오게 할 수 있는 $x_0$들의 확률분포는 무엇일까?
• 우리는 $x_0$의 최대 likehood를 구하고자 하는 것으로 생각할 수 있음.
• 최종적인 noise 형태 $p(x_T)$는 $\mathcal{N}(x_T;0,I)$ 를 따르고 여기서부터 reverse process를 수행!
• 그런데 말입니다. 현재 나는 $x_t$인데 과거 $x_{t-1}$의 분포를 어떻게 할 수 있지? 그래서 이걸 학습하자는 것이 핵심

$p_{\theta }(x_{0:T})=p(x_T){\prod }_{t=1}^T{p}_{\theta }(x_{t-1}\mid x_t)=p(x_T)\cdot p_{\theta }(x_{T-1}\mid x_T)\cdot p_{\theta }(x_{T-2}\mid x_{T-1})\cdots p_{\theta }(x_1\mid x_2)\cdot p_{\theta }(x_0\mid x_1)$ $p_{\theta }(x_{t-1}\mid x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t))$

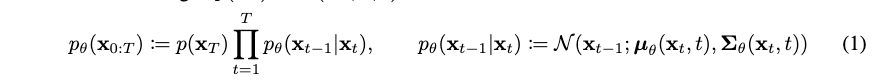
• $x_0$: 원본 데이터 (예: 깨끗한 고양이 사진)
• $x_{1:T}$: 노이즈가 점진적으로 추가된 잠재 변수들
• $p_{\theta }(x_{t-1}\mid x_t)$: 역방향 과정(Reverse process)에서 $x_t$로부터 $x_{t-1}$을 생성하는 확률
• ${\mu }_{\theta }(x_t,t)$: 역방향 과정에서 평균을 예측하는 신경망 → 즉, 우리가 배우고 알아야할 것은 $x_{t-1}$이 따르는 평균값만 예측할 수 있다면 우리는 과거를 추정할 수 있게 된다.
• ${\Sigma }_{\theta }(x_t,t)$: 역방향 과정에서 분산을 예측하는 신경망 → 그런데 forward에서 trick으로 인해 모든 과정의 variance는 1로 가정할 수 있게 되었음.

수식 (3): Training Optimization

• $P_{\theta }$ 를 어떻게 최적화할 수 있을까?

• 우리는 ELBO를 이용해서 negative log likelihood의 최대 bound를 낮춤으로써 최적화 할 수 있다.

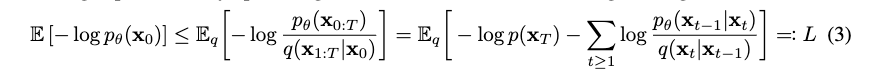
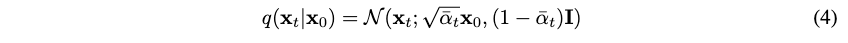
• (중요) $x_t$는 reparametric tric으로 인해서 $x_t=\sqrt{\overline{{\alpha }_t}}{x}_0+\sqrt{1-\overline{{\alpha }_t}}ϵ$ 으로 표현할 수 있다.

• 최종적으로 Loss term은 아래와 같이 정리 될 수 있다고 함

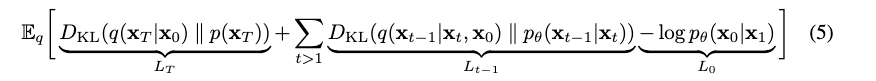
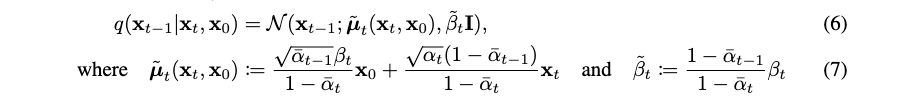
• 단 여기서 확인해야할 것은 $q$임. $q$는 diffusion procees인데, $q(x_{t-1}|x_t,x_0)$ 로 $x_t$가 given이지 않은가?

• 왜 이렇게 되는지에 대한 수식적인 증명은 appendix에 있으니 참고:)

결국 $P_{\theta }$ likelihood를 를 최대화하기 위해서는 위 수식 (5)을 줄이면 된다는 것인데, 이 term을 찬찬히 톫아보자.

(참조: https://www.youtube.com/watch?v=_JQSMhqXw-4&t=930s)

• 위 그림에서 $z=x_T$이다.
• Regularization term
  • $x_0$로 부터 diffusion process을 통해서 최종적으로 만들어진 데이터 분포와 noise $N(0,1)$의 분포가 닮을 수록 작아짐.
• Denoising term
  • forward process를 통해서 나온 $q(x_{t-1})$과 역으로 reverse해서 추정한 $P_{\theta }(x_{t-1})$의 분포가 같은가?
  • 여기서 $q$ 분포 식이 의아할 수 있으니, 이 또한 appendix에 정리되어 있으니 참고하시길.
• Reconstruction term
  • 원본 데이터로 복원할 log likelihood가 높을 수록 Loss가 작아짐
  • 다르게 표현하면 최종적으로 복원된 데이터가 원본과 동일한가?

3. Diffusion models and denoising autoencoder

• DDPM 논문은 이 복잡하고 어려운 Diffusion 최적화 수식을 denoising 관점에서의 Loss Function으로 단순화 시킨 것에 기여가 있음
• 이 복잡한 최적화 과정이
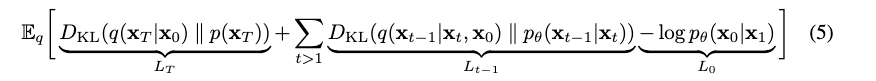
• 이렇게 바뀌게 된 것에 DDPM 논문의 기여가 있음
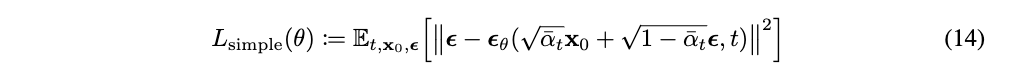
• 이 수식의 유도 과정은 직접 논문을 보고 따라가보기로 하고
• 결과적으로 정리된 최종 Loss term을 보면
• $t$ 시점에서 만들어진 $x_t=\sqrt{\overline{{\alpha }_t}}{x}_0+\sqrt{1-\overline{{\alpha }_t}}ϵ$ 를 모델의 입력으로 넣으면, 모델 ${ϵ}_{\theta }$이 noise $\theta$만 예측, 분리해 낼 수 있는지를 보는 Loss로 바뀜.
• 즉, 모델이 학습목표는 이전 단계의 데이터를 예측하는 것이 아니라, 제거해야할 noise를 예측하는 것으로 변했음.

• Algorithm 1: Training
• x1-(e1)-x2-(e2)-x3-(e3)-x4

x0=ecg
t = torch.randint(0, self.num_timesteps, (b,), device=device).long()
noise_e3 = default(noise, lambda: torch.randn_like(x_start))
x_t = self.q_sample(x_start=x0, t=t, noise=noise)
predicted_noise = self.model(x_t, t)
loss = F.mse_loss(predicted_noise, noise, reduction="none")

- model은 기본적으로 UNET을 사용하지만, 노이즈를 예측할 수 있다면 무슨 Network든 상관없음.
- 이를 통해서 보면 DDPM은 모델 네트워크 구조를 제안한 것이 아니라 학습 구조를 제안한 것임을 알 수 있음

• Algorithm 2: sampling

img = torch.randn(shape, device=device) #1
x_start = None
for t in reversed(range(0, self.num_timesteps)): #2
	img, x_start = self.p_sample(img, t)

def p_sample(self, x, t: int, x_self_cond=None, clip_denoised=True):
	b, *_, _ = *x.shape, x.device
	batched_times = torch.full((b,), t, device=x.device, dtype=torch.long)
	model_mean, _, model_log_variance, x_start = self.p_mean_variance(
	x=x, t=batched_times, x_self_cond=x_self_cond, clip_denoised=clip_denoised)
	
	noise = torch.randn_like(x) if t > 0 else 0.0 # no noise if t == 0
	pred_img = model_mean + (0.5 * model_log_variance).exp() * noise
	
	return pred_img, x_start

$p_{\theta }(x_{t-1}\mid x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t))$

• ${\mu }_t={\mu }_{\theta }(x_t,t)$
• ${\sigma }_t={\Sigma }_{\theta }(x_t,t))$

논문 수식	코드	설명
$x_{t-1}={\mu }_t+{\sigma }_{t}z$	pred_img = model_mean + (0.5 * model_log_variance).exp() * noise	다음 상태 $x_{t-1}$을 예측
$\mu =\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t)\right)$	model_mean	모델이 예측한 평균
${\sigma }_t=\sqrt{\text{posterior variance}}$	(0.5 * model_log_variance).exp()	분산을 활용해 표준편차 계산
$z\sim \mathcal{N}(0,I)$	noise = torch.randn_like(x) if t > 0 else 0.0	가우시안 노이즈 샘플링

Results

Transclude of diffusion_animation